TDT4287 - Algoritmer for bioinformatikk

Sources and syllabus

An Introduction to Bioinformatics Algoritms
- Chapters ?
Algorithms on Strings, Trees, and Sequences (Gusfield)
- Chapters 3, 4, 5-6.1 and 7.1-7.10
Statistical Methods in Bioinformatics. (Ewens & Grant)
- Chapters 4, 10 and 11
How do RNA folding algorithms work? (Eddy)
Complete Suboptimal Folding of RNA and the Stability of Secondary Structures. (Wuchty et al.)

01 Introduction

Bioinformatics - the collection, classification, storage, and analysis of biochemical and biological information using computers especially as applied in molecular genetics and genomics.

This course will focus on sequence (string) analysis

Alignment -> finding similar sequences
Suffix trees -> index-based searching
Motif finding -> similarities between sequences
Assembly -> reconstructing sequences from fragments
RNA structures -> similarities within a sequence

A cell as seen by a computer scientist

\text{DNA} \longrightarrow_{f_{TR}} \text{RNA} \longrightarrow_{f_{TL}} \text{Protein}

DNA replicates itself
$f_{TR}$ is the transcription of DNA to RNA
$f_{TL}$ is the translation of RNA to Protein

List of biological sequence problems

How do genes encode proteins?
What is the function of a protein?
How do we recognize genes in DNA?
How are genes controlled so that proteins are produced at the correct place and time?

How do genes encode proteins?

Protein structure

Sequence (string) of amino acids
- 20 different amino acids
Amino acid sequence folds into unique, reproducible 3D (tertiary) structure
The structure determines the function

The genetic code

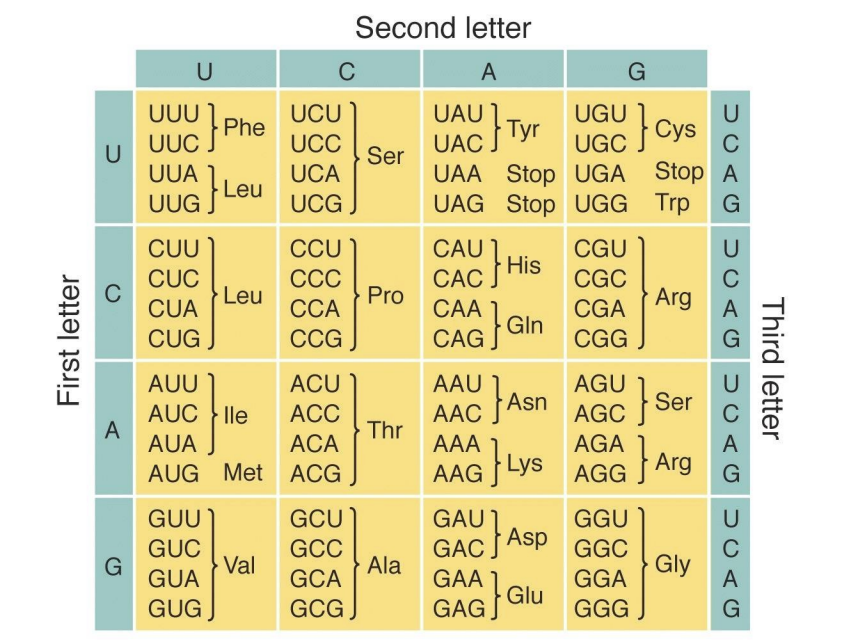
The genetic code must use at least 3 nucleotides to encode all 20 amino acids, but will have some redundancy ( $4^3 = 64$ ).

What is the function of a protein?

Protein sequence determines function.

\text{Sequence} \longrightarrow \text{Structure} \longrightarrow \text{Function}

Genes evolved from common ancestor - homologs - often have similar functions. Thus, we can search for similar gene sequences to determine similar gene functions. We determine similar genes by finding common gene subsequences.

Longest common subsequence (LCS)

E.g. the LCS of AGCTAGCT and ATGCATGC is AGCAGC.

Recursive LCS

Three possibilities:

Last letter from both strings part of LCS if identical; none of them otherwise
Last letter from left string is part of LCS
Last letter from right string is part of LCS

Thus we have

\begin{align*} \text{LCS}_{(x,y)} &= \max\{ \\ & \text{LCS}_{(x,y-1)}, \\ & \text{LCS}_{(x-1,y)}, \\ & \text{LCS}_{(x-1,y-1)} + (\text{LCS}[x] == \text{LCS}[y] \; ? \; 1 : 0) \\ & \} \end{align*}

Recursive LCS solves subproblems multiple times.

Dynamic programming (DP) LCS

Dynamic programming can be applied to recursive LCS such that subproblems are only solved once. We solve the matrix bottom-up. To record the actual subsequence, we also build a backtrack matrix.

// LCS(S, R)

a[0,0] = 0
for i in range(1, |S|):
    a[i,0] = 0
for j in range(1, |R|):
    a[0,j] = 0
for i in range(1, |S|):
    for j in range(1, |R|):
        a[i,j] = max{
            a[i-1,j],
            a[i,j-1],
            a[i-1,j-1] + (s[i] == r[j] ? 1 : 0)
        }
        // The following creates the backtrack matrix
        b[i,j] = {
            0 if a[i,j] == a[i-1,j],        // "up"
            1 if a[i,j] == a[i,j-1],        // "left"
            2 if a[i,j] == a[i-1,j-1] + 1   // "up-left"
        }

// PrintLCS(b, S, i, j):

if i == 0 or j == 0:
    return
if b[i,j] == 2:
    PrintLCS(b, S, i-1, j-1)
    print s[i]
else if b[i,j] == 0:
    PrintLCS(b, S, i-1, j)
else:
    PrintLCS(b, S, i, j-1)

Homework

Compute the LCS DP matrix for LCS(ATTCGGTTA, TAGTGATG).
Find the LCS without using a backtrack matrix.
LCS(AGCTTAGCTG, TCGGATG) has multiple solutions (for example, TTG or ATG). Find an algorithm that returns all the LCSs. (Hint: a stack could be useful)

02 Alignment

Subsequences

A subsequence is an ordered sequence of characters from a string. They characters do not have to be consecutive in the original string. We may represent a subsequence as an ordered set of indexes.

A common subsequence of two strings is a subsequence of both strings.

Algorithms have already been discussed in chaper 01 Introduction. // TODO: Move and join

Edit distance (ED)

The Levenshtein edit distance between two strings S and R is the minimum number of edit operations (insertions, deletions, substitutions) for transforming S to R.

Recursive ED may be optimized by dynamic programming.

Edit operations model evolutionary events. Edit distance-based comparisons measure evolutionary distance. Alignments visualize evolutionary changes.

Global alignment (GA)

Find the best alignment between S and R given a scoring function.

Local alignment (LA)

Find the best local alignment between S and R given a scoring function. Output: Substrings of S and R with maximal global alignment of all substrings of S and R

Local alignment is useful when changes are not uniform across sequence

Local/Global alignment variants

Best complete match within a longer string (e.g. |S| >> |R|)
Best alignment between prefix of S and suffix of R
Repeated matches above T within a longer string
Regions with different scoring functions
- Regions without gaps vs. Regions with gaps
- Protein regions with different physical characteristics

03 Heuristic alignment

04 Substring indexes

Exact pattern matching

Text T
|T| = m
Ex: “I like bananas and potatoes”
Pattern P
|P| = n
Ex: “banana”

Find all occurrences of P in T
- Naive: O(mn)
- Possible: O(m + n)

courses/tdt4287 ✨

Table of Contents