Økonomi og regnskap

13 Mikroøkonomi og markedsformer (s. 277-314)

13.1 Etterspørsel

Etterspørsel uttrykker en sammenheng mellom prisen $P$ på et produkt og den mengden som etterspørres av produktet $Q(P)$. Indirekte etterspørsel er den inverse funksjonenen $P(Q)$.

Totalinntekt $TR$ er mengden vi selger $Q$ ganget med prisen $P(Q)$. Merk at dersom det er flere aktører kan deres mengde påvirke prisen.

$$TR_0(Q_0) = Q_0 \cdot P(Q_0 + Q_1)$$

Marginalinntekt er den ekstra inntekten en man får ved å produsere og selge én enhet mer. Maksimal inntekt er gitt ved $MR(Q) = 0$

$$MR(Q) = \frac{d}{dQ} TR$$

Etterspørselselastisitet eller priselastisitet er forholdet mellom den relative endringen i $Q$ og den relative endringen i $P$

$$\epsilon = - \frac{dQ}{dP} \cdot \frac{P}{Q}$$

• Priselastisk: $\epsilon > 1$ betyr at $TR$ øker når $P$ synker.
• Prisuelastisk: $\epsilon < 1$ betyr at $TR$ synker når $P$ synker
• Enhetselastisk: $\epsilon = 1$ betyr at $TR$ er konstant med hensyn på $P$.

Dette gir oss også et annet uttrykk for $MR$

$$MR(Q) = P(Q) \cdot \left( 1 - \frac{1}{\epsilon} \right)$$

Gjennomsnittsinntektene $AR(Q)$, også kalt enhetsinntektene er totale inntekter delt på mengden.

$$AR(Q) = \frac{TR(Q)}{Q} = P(Q)$$

13.2 Tilbud og markedslikevekt

Tilbud uttrykker en sammenheng mellom prisen $P$ på et produkt og den mengden som markedet tilbyr av produktet $Q(P)$. Når et marked er i balanse, vil etterspørsels- og tilbudsfunksjonen møtes i ett enkelt punkt - likevektspunktet.

13.3 Kostnader

Variable kostnader $VC(Q)$ er kostnader som avhenger av mengden produsert, for eksempel lønn og pris på råvarer. Faste kostnader $FC$ er kostnader som er uavhengige av mengden, for eksempel vedlikehold av lokaler og maskiner. Totale kostnader $TC(Q)$ er summen av faste og variable kostnader.

Marginalkostnadene $MC(Q)$ uttrykker kostnaden ved å produsere én enhet mer.

$$MC(Q) = \frac{d}{dQ} TC$$

Gjennomsnittskostnadene $AC$, også kalt enhetskostnadene er totale kostnader delt på mengden.

$$AC(Q) = \frac{TC(Q)}{Q}$$

Vi kan minimere kostnadene per enhet ved å finne bunnpunktet til $AC(Q)$

$$\frac{dAC(Q)}{dQ} = 0 \implies MC(Q) = AC(Q)$$

Profitt $\Pi(Q)$ er differansen mellom totale inntekter og totale kostnader

$$\Pi(q) = TR(Q) - TC(Q)$$

Vi maksimerer profitt ved å finne toppunktet

$$\frac{d\Pi(Q)}{dQ} = 0 \implies MR(Q) = MC(Q)$$

13.4 Ulike markedsformer

Vi kaller markeder med bare én produsent for monopoler, markeder med to kalles duopoler og markeder med få produsenter (to eller flere) kalles oligopoler. Et marked med veldig mange produsenter kalles et frikonkurransemarked.

Frikonkurransemarked

Kriterier

• Veldig mange produsenter
• Konsumentene har god kunnskap om kvaliteten på varene som tilbys

Konsekvenser

• Prisen $P$ er konstant med hensyn til en enkelt produsents mengde $Q$
• Elastisiteten $\epsilon$ er tilnærmet uendelig
• $MR = P$
• Maksimal profitt er gitt ved $MC(Q) = P$

Monopol og dødvektstap

Kriterier

• Kun én produsent, svært mange konsumenter

Konsekvenser

• Etterspørselen produsenten opplever er den samme som etterspørselen til hele markedet
• Maksimal profitt er gitt ved $MC(Q) = MR(Q)$

Statlige monopoler og veldedige organisasjoner vil kanskje tilpasse seg til $\Pi = 0$.

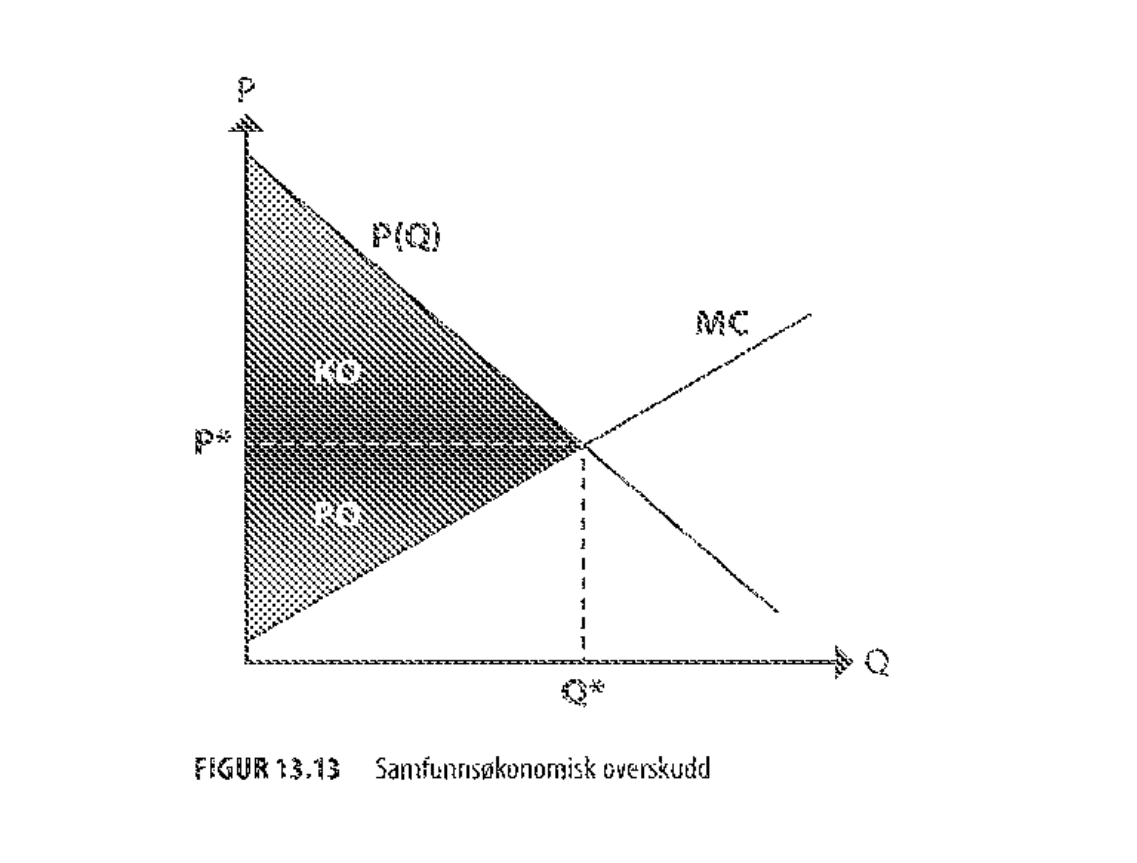
Konsumentoverskudd $KO$ er forskjellen mellom det konsumentene faktisk betaler og det de maksimalt hadde vært villige til å betale.

$$KO = \int_0^Q P(q)dq - TR(Q)$$

Produsentoverskudd $PO$ er forskjellen mellom inntekter og variable kostnader.

$$PO = TR(Q) - \int_0^Q MC(q)dq$$

Samfunnsøkonomisk overskudd $SO$ er summen av konsumentoverskudd og produsentoverskudd. Dette er størst når $P(Q) = MC(Q)$, altså under frikonkurranse.

$$SO = KO + PO = \int_0^Q P(q) - MC(q) dq$$

Dødvektstapet er gitt ved maksimal samfunnsøkonomisk overskudd minus faktisk samfunnsøkonomisk overskudd.

$$\int_Q^{Q_{SO}} P(q) - MC(q) dq$$

Duopoler og oligopoler

I en Nash-likevekt er alle spillerne fornøyd med eget strategivalg gitt alle andre spilleres valg av strategi.

Cournot-modellen: Anta

• $MC_1 = MC_2 = C$
• $P_1(Q) = P_2(Q) = A - BQ$
• $Q = Q_1 + Q_2$.

Da er

$$Q_1 = \frac{A - BQ_2 - C}{2B}.$$

Dersom $Q_1 = Q_2$ har vi

$$Q_1 = Q_2 = \frac{A-C}{3B}$$

13.5 Mikroøkonomisk teori som modellapparat

Et viktig teoretisk resultat viser at markeder under visse betingelser vil gi løsninger som er optimale for samfunnet på den måten at ingen kan få det bedre uten at noen andre får det dårligere. Dette kalles en paretooptimal tilpasning. Kriterier:

• Antallet produsenter og konsumenter må være svært stort
• Alle produsenter og konsumenter må opptre økonomisk fornuftig
• Alle aktører i markedet må ha perfekt informasjon om kostnader og nytte i markedet
• Det må ikke eksistere transaksjonskostnader
• Det må ikke være noen eksterne effekter

14 Regnskapsanalyse og økonomistyring (s. 315-366)

14.1 Grunnleggende regnskapsbegreper

Regnskapet er bedriftens hovedredskap for å følge med på kostnader og inntekter bedriften har hatt i en periode.

Moderne bedrifter benytter dobbel bokføring. Alle poster føres opp på to ulike T-kontoer, på den ene som et debet-beløp (venstre kolonner) og på den andre som kredit-beløp (høyre kolonner). Debet er normalt et beløp man har ervervet seg eller eier, men det kan også representere en nedbetaling av gjeld eller reduksjon av egenkapitalen. Kredit representerer en reduksjon av eiendeler eller en økning av gjeld eller egenkapital. I resultatregnskapet betegner debet kostnader som har påløpt, og kredit inntekter man har hatt. Ved regnskapsslutt summeres alle T-kontoene, eventuelle restbeløp på kredit- eller på debet-siden kan føres direkte ut til resultatregnskapet og balansen.

Kostnadsbegreper

• En kostnad er bruk av en ressurs som bedriften har brukt for å få til noe, som på et eller annet tidspunkt har ledet eller vil lede til en inntekt.
• En utgift er en pådratt betalingsforpliktelse.
• Utbetaling er når du betaler denne utgiften, altså at du innfrir en betalingsforpliktelse.
• Totalkostnader dekker alle kostnader som har påløpt i en regnskapsperiode.
• Rentekostnader er renter vi betaler for lån og kassakreditter vi har.
• Finansielle kostnader er knyttet til finansielle transaksjoner vi gjør, men omfatter ikke renter - f.eks. gebyrer.
• Ekstraordinære kostnader skyldes spesielle hendelser som ikke kan sies å være en del av den vanlige driften i regnskapsåret.
• Beslutningsrelaterte kostnader
  • Alternativkostnad representerer hva vi kunne hatt av inntekter ved en alternativ plassering av pengene.
  • Sunk costs/tapte kostnader er penger vi har brukt som vi ikke kan få tilbake i en beslutningssituasjon.
• Tilvirkningskostnad $TK = dM + MO + dL + TO$

I tillegg har vi variable kostnader, faste kostnader, marginalkostnad og gjennomsnittskostnad som er definert tidligere.

14.2 Finansregnskapet

Finansregnskapet er lovpålagt for de fleste selskaper, og lages hovedsakelig for å gi eksterne parter en innsikt i hvordan selskapet drives og hva det har oppnådd. I finansregnskapet opererer vi med to hoveddokumenter. Resultatregnskapet viser hva selskapet har hatt av inntekter og kostnader i perioden (ofte et år). Balansen viser hvordan selskapets kapital er fordelt på ulike poster ved periodeavslutning.

Balansen er en oppstilling av eiendeler på den ene siden, og hvordan disse eiendelene er finansiert på den andre siden.

14.3 Grunnleggende regnskapsanalyse av finansregnskapet

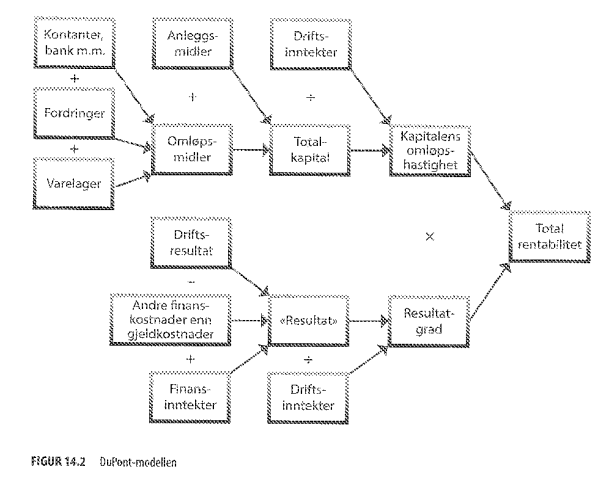
Å se på totalrentabiliteten $R_{TK}$ er den vanligste lønnsomhetsanalysemetoden. Den forteller hvor mange prosent inntjening bedriften har på den totale kapitalen benyttet i regnskapsåret. For andre bedrifters regnskap bruker vi følgende formel

$$R_{TK} = \frac{\text{Driftsresultat} + \text{Finansinntekter}}{\text{Gjennomsnittlig totalkapital}}$$

For eget regnskap er det bedre å bruke DuPont-modellen, som er mer komplisert, men gir også betydelig mer informasjon.

Egenkapitalrentabilitet viser investorer hvor god avkastning de får på sine investerte penger og er gitt ved

$$R_{EK} = \frac{\text{Driftsresultat}}{\text{Gjennomsnittlig egenkapital}}$$

Soliditet er knyttet til egenkapitalandelen.

Rentedekningsgrad er gitt ved

$$\text{Rentedekningsgrad} = \frac{\text{Driftsresultat} + \text{Finansinntekter}}{\text{Finanskostnader}}$$

Likviditetsgrad

Likviditet handler i stor grad om forholdet mellom anleggsmidler (langvarige fysiske eiendeler) og omløpsmidler (eiendeler som lett kan gjøres om til kontanter).

$$\text{Likviditetsgrad 1} = \frac{\text{Omløpsmidler} + \text{Ubenyttet kassakreditt}}{\text{Kortsiktig gjeld}} > 2$$

$$\text{Likviditetsgrad 2} = \frac{\text{Mest LOM*} + \text{Ubenyttet kassakreditt}}{\text{Kortsiktig gjeld}} > 1$$

* $\approx \text{Omløpsmidler} - \text{Varelager}$

Arbeidskapital er differansen mellom omløpsmidler og kortsiktig gjeld. Hvis denne er negativ har vi finansiert noe av anleggsmidlene med kortsiktig gjeld, som kan tyde på dårlig likviditet.

14.4 Internregnskapet

Internregnskapet er ikke lovpålagt, men de fleste større selskaper har ulike typer av internregnskap som et middel for ledelsen til å styre økonomi og produksjon i selskapet.

Kalkyler brukes ofte som navn på en forhåndsberegning av hva fortjenesten er på et bestemt produkt eller en produktgruppe.

Det fins to hovedretninger innen kalkyler: selvkostmetoden og bidragsmetoden. Selvkostmetoden bruker tilleggssatser for å kalkulere både faste og variable kostnader, mens vi etter bidragsmetoden kun kalkulere inn variable kostnader.

I en selvkostkalkyle tar vi med alle indirekte kostnader. Dette gir den laveste prisen for langsiktig overlevelse.

I en bidragskalkyle tar vi kun med variable kostnader. Dette gir den laveste prisen for en kortsiktig fordel. Dette er ekvivalent med å finne dekningsbidraget (?).

Dekningsbidrag og dekningsgrad

$$\text{Dekningsbidrag per stk.} = \text{Salgspris per stk.} - \text{Variable kostnader per stk.}$$

$$\text{Totalt dekningsbidrag} = \text{Totale salgsinntekter} - \text{Totale variable kostnader}$$

$$\text{Dekningsgrad} = \frac{\text{Dekningsbidrag}}{\text{Salgspris}}$$

Nullpunktsanalyser

De fleste resultater i nullpunktsanalyse kan utledes fra

$$TR(Q) = TC(Q)$$

Vi har følgende

$$\text{Nullpunkt i kr.} = \frac{\text{Faste kostnader}}{\text{Dekningsgrad}}$$

$$\text{Nullpunkt i stk.} = \frac{\text{Faste kostnader}}{\text{Dekningsbidrag per stk.}}$$

$$\text{Sikkerhetsmargin i kr.} = \text{Dagens omsetning i kr.} - \text{Nullpunkt i kr.}$$

$$\text{Sikkerhetsmargin i stk.} = \text{Dagens omsetning i stk.} - \text{Nullpunkt i stk.}$$

$$\text{Sikkerhetsmargin i \%} = \frac{\text{Sikkerhetsmargin i stk./kr.}}{\text{Dagens omsetning i stk./kr.}}$$

$$\text{Målsatt salg i kr.} = \frac{\text{Faste kostnader} - \text{Ønsket overskudd}}{\text{Dekningsgrad}}$$

14.5 Budsjettering

Kostnadsbudsjettet informerer ledelsen om hvor mye penger som er brukt så langt i et prosjekt eller en tidsperiode.

Resultatbudsjettet brukes for å simulere en periode, og bruker de samme postene som i resultatregnskapet. Det ser på både inntekter og kostnader.

Likviditetsbudsjettet er også en slags gjetning om hvordan man vil ligge an fremover i tid, men er kun opptatt av bedriftens likviditet. Det ser på inn- og utbetalinger, samt kundefordringer.

15 Investeringsanalyse (s. 367-422)

15.1 Investeringer

En investering kan defineres som å bruke ressurser i dag for å skaffe seg bedre ressursgrunnlag i fremtiden.

15.2 Nåverdiberegninger

Alternativkostnaden til kapital bestemmes av hva som er den beste alternative avkastning med samme risiko. Vi kaller dette en målestokk fordi vi sammenligner investeringen vår med denne alternative plasseringen.

Avkastningskrav, forventet avkastning, eller diskonteringsrenten er betegnet $r$.

Nominell rente $r_N$ er rente i penger, realrente $r_R$ er rente i verdi (med hensyn til inflasjon).

$$r_N = r_R + \text{infl.} + r_R \cdot \text{infl.}$$

Nåverdien av fremtidige kontantstrømmer er gitt som følger. $k_t$ er innbetalinger minus utbetalinger i periode $t$. $k_0$ er gjerne negativ siden vi investerer et beløp.

$$NV = \sum_{t=1}^N \frac{k_t}{(1+r_t)^t}$$

Er $k_t$ konstant lik $k$ har vi

$$NV = k \frac{1-(1+r)^{-N_e}}{r}$$

Nettonåverdien er gitt ved

$$NNV = k_0 + NV$$

Nåverdiskvoten er gitt ved $\frac{NNV}{-k_0}$ Denne brukes til å sammenlikne investeringer når det er mangel på kapital.

Internrenten er den diskonteringsrenten som gir $NNV = 0$. Dette er en følsomhetsanalyse av renten.

Annuitet brukes til å sammenlikne investeringer med forskjellige levetider, som kan gjentas. Gjentas de uendelig sammenlikner vi $\text{annu}/r$.

$$\text{annu} = NNV \frac{r}{1-(1+r)^{-N_e}}$$

For kontantstrømmer som begynner som $k$ vokser med en gitt prosent $g$ over uendelig tidsperioder har vi

$$NV = \lim_{N\rightarrow\infty}\sum_{t=1}^N \frac{k(1+g)^{t-1}}{(1+r)^t} = \frac{k}{r-g}$$

Tilbakebetalingstiden $PB$ er minste antall perioder som gir $NNV \geq 0$ Dersom $k_t$ er konstant $k$ er $PB = -k_0 / k$

15.3 Risikoanalyse

Følsomhetsanalyse går ut på å variere én parameter av gangen og se på effekt på $NNV$.

Scenarioanalyse går ut på å variere flere parametre samtidig og se på effekt på $NNV$.

Med en Monte Carlo-simulering kan vi beregne forventet $NNV$ basert på sannsynlighetsfordelinger til parametre.

Beslutningstrær fremstiller prosjektet som en rekke beslutninger og utfall, modellert som et tre med vektede kanter.

15.4 Risiko og avkastning

$$\sigma_r^2 = Var[r] = E[(r - E[r])^2]$$

$$\sigma_r = Std[r] = \sqrt{Var[r]}$$

$$\sigma_{zy} = Cov[z,y] = E[(\tilde{z}-z)(\tilde{y}-y)]$$

$$Var[az] = a^2Var[z]$$

$$Var[z + y] = Var[z] + Var[y] + 2Cov[z,y]$$

$$Var[\text{portefølje}] = x_i^2\sigma_i^2 + x_j^2\sigma_j^2 + 2x_ix_j\sigma_{ij}$$

$$\text{Korrelasjonskoeffisienten } \rho_{ij} = \frac{\sigma_{ij}}{\sigma_i \sigma_j}$$

Diversifisering innebærer at porteføljerisiko blir lavere enn det veide gjennomsnittet av risikoene, så lenge det ikke er perfekt positiv korrelasjon. Samtidig er forventet avkastning alltid lik det veide gjennomsnittet av forventede avkastninger.

$$Var[p_{1,2,\dots}] = \sum_{i=1}^N \sum_{j=1}^N x_i x_j \sigma_{ij}$$

$$\text{Porteføljerisiko} = \text{Diversifiserbar risiko} + \text{Markedsrisiko}$$

Beta

$$\beta_i = \rho_{im} \frac{\sigma_i}{\sigma_m}$$

En fullt diversifisert portefølje av investeringer har standardavviket

$$\sigma^* = \beta \sigma_m$$

Diversifiserbar risiko for en portefølje er gitt ved

$$\sigma^2 - (\sigma^{*})^2$$

Standardavviket til en portefølje kan aldri være større enn det største standardavviket i porteføljen.

15.5 Capital Asset Pricing Model - CAPM (Kapitalverdimodellen - KVM)

CAPM er den mest brukte formelle metoden for prising av risiko i investeringsprosjekter.

For en aksjeportefølje av to aksjer er forventet avkastning og standardavvik gitt ved følgende

$$r_s = xr_1 + (1-x)r_2$$

$$\sigma_s = \sqrt{x^2\sigma_1^2 + (1-x)^2\sigma_2^2 + 2x(1-x)\rho_{12}\sigma_1\sigma_2}$$

For kombinasjon med en risikofri investering er standardavviket gitt ved følgende, der $\alpha$ er andelen av formuen som plasseres i aksjeporteføljen

$$\sigma = \alpha\sigma_s$$

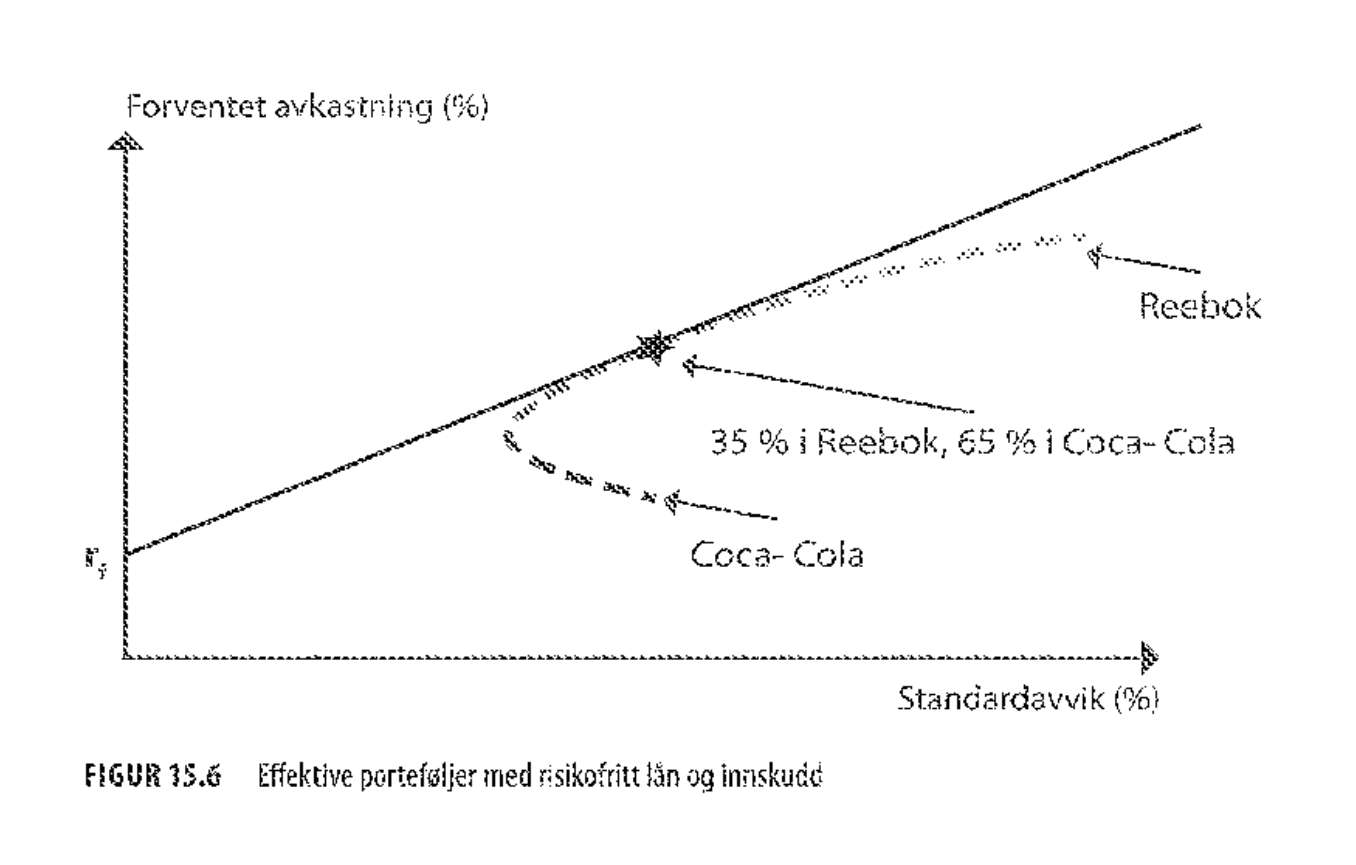
Linjen som går fra risikofri rente og tangerer kurven representerer effektive porteføljer og kalles kapitalmarkedslinjen.

Videre ser vi på vilkårlig mange aksjer. Da får vi en verdipapirmarkedslinje som også fanger opp risikopremien til enkelte verdipapirer.

Investeringer som omsettes i velfungerende markeder må ligge på verdipapirmarkedslinjen der risikopremier bestemmes av beta. $r_m - r_f$ kalles markedsrisikopremien.

$$r = r_f + \beta (r_m - r_f)$$

Sharpe Ratio er et mål på risikojustert avkastning og er gitt ved

$$SR = \frac{r - r_f}{\sigma}$$

Bruk av CAPM

• Beta $\beta$ kan finnes ved linær regresjon mellom avkastninger på en investering og avkastninger på en bred markedsindeks
• Risikofri avkastning $r_f$ kan vi finne som avkastning på statsobligasjoner av passende lengde
• Forventet markedsavkastning $r_m$ finner vi som risikofri avkastning pluss historisk forventet markedspremie

15.6 Selskapets kapitalkostnad - WACC

Vi har følgende hovedmuligheter til finansiering:

• Ny egenkapital
• Tilbakeholdt overskudd
• Lån
• Hybridmodell

Vi finner kan finne kapitalkostnad ved formelen

$$r_A = \frac{D}{V} r_D + \frac{E}{V} r_E$$

• $E$, verdien av egenkapital, finnes fra markedsverdier av aksjer ganger antall utestående aksjer. Evt totalkapital - gjeld.
• $r_E$, forventet avkastning av egenkapital, kan finnes via CAPM med regresjonsbeta.
• $D$, børsnotert obligasjonsgjeld
• $r_D$ avkastning på gjeld

Dersom analysen bygger på CAPM kan vi uttrykke beta for aktiva som følger:

$$\beta_A = \frac{D}{V} \beta_D + \frac{E}{V} \beta_E$$

Weighted average cost of capital - WACC - er kapitalkostnaden til totalkapitalen etter skatt (skattefordel). Denne kan brukes som diskonteringsrente for prosjekter.

$$WACC = \frac{D}{V}(1-T_C) r_D + \frac{E}{V} r_E$$

15.7 "Giring" - bruk av lån til å øke egenkapitalrenabiliteten

M&M 1: Selskapet kan ikke endre sin totale verdi ved å splitte kontantstrømmene. Verdien er bestemt av selskapets realinvesteringer, ikke av hvilke verdipapirer det utsteder.

M&M 2: Forventet avkastning på egenkapitalen til et selskap øker med gjeld-egenkapital-forholdet, uttrykt i markedsverdier, og hastigheten i økningen er bestemt av spredningen mellom $r_A$ og $r_D$.

Static trade-off sier at verdien av selskapet vil variere med giringen og den kan uttrykkes som følger

$$\text{Verdi av selskap} = \text{Verdi gitt kun egenkapitalfinansiert} + \text{Nåverdi av skattefordel av gjeld} - \text{Nåverdi av konkurskostnader}$$

Giring kan også bli påvirket av andre vurderinger enn de rent økonomiske

• Kontroll: Å øke egenkapitalen ved å utstede aksjer reduserer eiernes kontroll, gjeld holder kontrollen
• Fleksibilitet: Lånekapital og tilbakeholdt overskudd er raskere enn ny egenkapital
• Eksisterende gjeldsgrad: har betydning for mulighet og rente for fremtidige lån

15.8 Kvalitative metoder for evaluering av Investeringer

Med kvalitet mener vi i denne sammenhengen ikke hvor bra investeringen blir, men hvor godt den samsvarer med bedriftens strategiske plan, og hvor godt den faktisk utnytter bedriftens tilgjengelige ressurser.

15.9 Forventning, standardavvik, varians, kovarians